Designing and Implementing an Innovative Ideal Course Path Algorithm

Published on August 25, 2024

Choosing the right courses to take each quarter is a challenging task for many university students, especially those at a university like Cal Poly, which offers a wide array of courses with various requirements. As a Computer Science student, I realized the need for an automated tool that could help students navigate this complex decision-making process. This blog post details the development of an algorithm I implemented in Java to find the ideal course path for students. This algorithm is a prototype tailored to my specific needs, but it can be generalized for broader use.

Problem Description

The goal of this algorithm is to generate an optimal course schedule that helps a student complete their degree requirements in the shortest possible time. The algorithm considers various factors, such as courses already taken, remaining requirements, and the number of courses a student is willing to take each quarter. While this prototype does not handle prerequisites, it could be easily extended to include them in the future.

Algorithmic Approaches

I implemented four different methods to solve the problem of course scheduling. Two of these methods aim to find an ideal solution, while the other two provide approximate solutions. Below, I’ll explain each method and its underlying algorithms.

1. Naive Course Path Finder

The first method I implemented was a simple and straightforward approach. This algorithm divides the courses based on the quarters in which they are offered and randomly selects a course list that meets the seasonal requirements. The selected courses should fulfill the student's requirements. While this approach is easy to implement, it is not optimized, leading to potentially suboptimal results. For instance, using this method, I would need to take extra units, possibly delaying my graduation by a full year.

2. Brute Force Search

The brute force method exhaustively searches through all possible course combinations to find the optimal path. While this method guarantees an optimal solution, it is computationally expensive. The search space grows exponentially with the number of courses and seasons, making it impractical for real-world use. In fact, for most students, the algorithm would take longer to complete than the age of the universe!

3. Divide and Dynamic Programming (Divide and DP)

The third approach leverages a divide-and-conquer strategy combined with dynamic programming. The algorithm begins by dividing the course load across seasons based on the student’s preferences and the current time of year. Then, it uses dynamic programming to find the ideal course list for each season, considering the student's past course history and remaining requirements.

However, this approach has limitations. For instance, if the algorithm selects a course in one season that fulfills multiple requirements, it might miss a more optimal combination across other seasons. This is because the algorithm optimizes for each season independently, without considering the interdependencies between seasons.

4. Dynamic Programming and Divide (DP and Divide)

The final and most effective method I implemented is the "DP and Divide" algorithm. Unlike the previous approach, this method first finds the optimal course list without considering the seasons. It then divides the selected courses across seasons in the most efficient way.

This algorithm uses dynamic programming to solve a problem similar to the knapsack problem, where the goal is to maximize the number of requirements fulfilled with the least number of courses. Each course is treated as an item with a "weight" of 1, and each requirement fulfilled adds to the "value" of the item.

dp[i, j] = max number of requirements fulfilled with i courses using course j

Finding the Ideal Course Path

The dynamic programming algorithm treats the problem as a knapsack-like problem where each course can fulfill one or more requirements, and the goal is to maximize the requirements fulfilled while minimizing the number of courses.

Each entry in the DP table stores a list of requirements fulfilled by a certain number of courses and the courses used to fulfill them. The final solution is the maximum value found in the DP table after considering all courses.

Distributing Courses Among Seasons

After determining the optimal set of courses, the next challenge is distributing these courses across the available quarters. This is where the Ford-Fulkerson method, specifically the Edmonds-Karp algorithm, comes into play.

Ford-Fulkerson Method (Edmonds-Karp Algorithm)

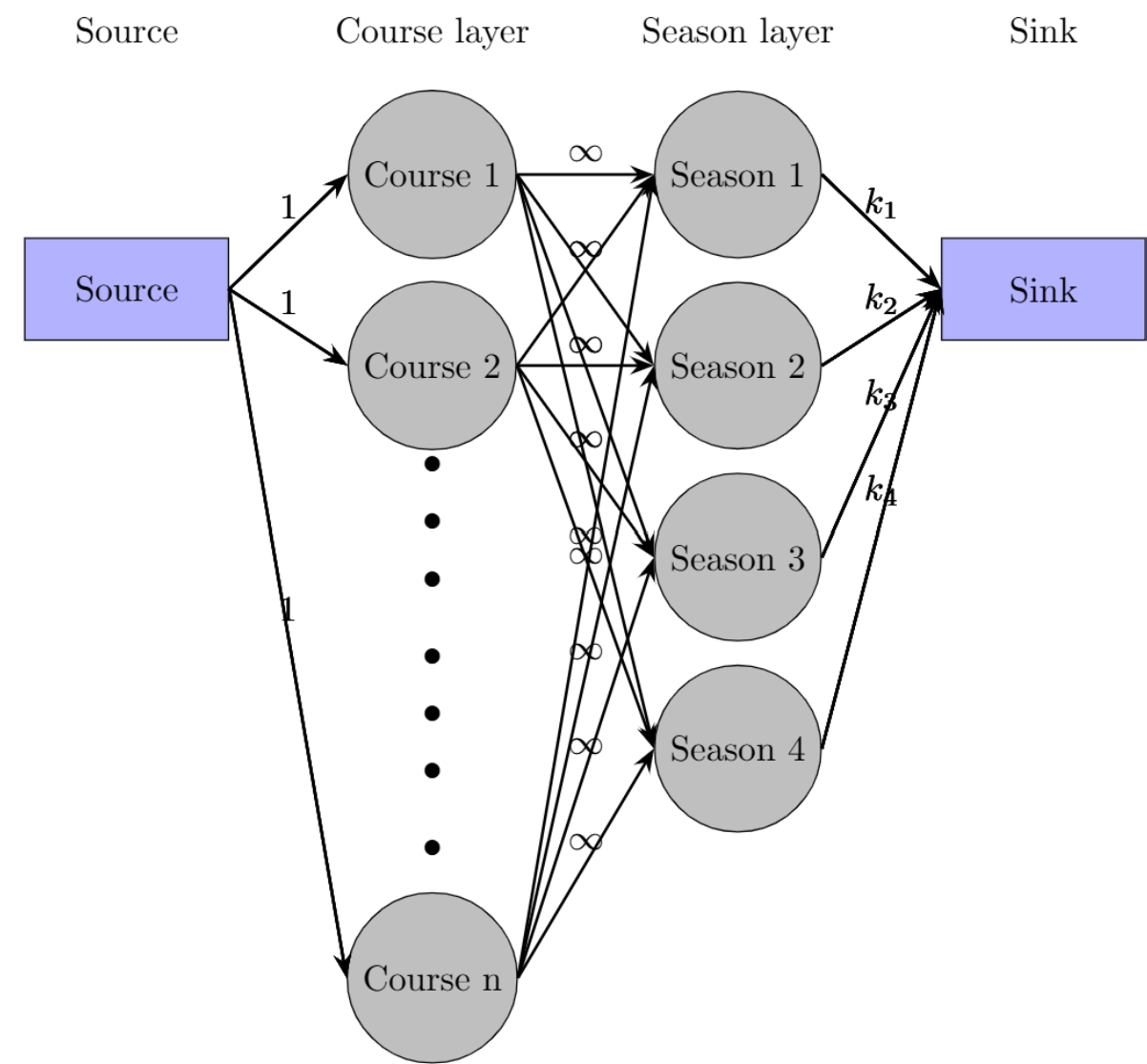
To model the problem of distributing courses across quarters, I represented it as a flow network:

• Each course is represented as a node.
• Each quarter (season) is also a node.
• There is a source node connected to each course node with an edge of capacity 1.
• Each course node is connected to season nodes with an edge of infinite capacity.
• Season nodes are connected to a sink node with edges corresponding to the capacity (number of courses the student can take) of each season.

The goal is to find the maximum flow in this network, which corresponds to the maximum number of courses that can be optimally distributed across the seasons. The Edmonds-Karp algorithm uses Breadth-First Search (BFS) to find augmenting paths in the residual graph, adjusting the flow until no more augmenting paths are found.

Residual Graph

The residual graph is crucial in this process, as it tracks the remaining capacity for additional flow. For each edge in the network, the residual graph includes a forward edge with the remaining capacity and a backward edge with the flow already used. The algorithm iteratively adjusts these edges until the optimal distribution is achieved.

    for each edge (u, v) in the augmenting path:
        residual_forward_edge_c(u, v) = capacity(u, v) - flow(u, v)
        residual_backward_edge_c(v, u) = flow(u, v)
        flow(u, v) += min_capacity
        flow(v, u) -= min_capacity
    

Conclusion

By implementing these algorithms, I was able to design a tool that helps me and potentially other students find the optimal course path, minimizing the time to graduation. The dynamic programming and Ford-Fulkerson algorithms provided substantial improvements over naive and brute-force methods, both in terms of efficiency and practicality.

The code for this tool is available on GitHub, and detailed comments are provided for each part of the implementation. While this is an alpha version tailored to my own course requirements, I hope it can be generalized and used by other students to ease the process of course selection.

Back to Blog